Understanding Factorisation In Maths Class 8: A Comprehensive Guide

Factorisation in maths Class 8 is all about breaking numbers or expressions into simpler parts, making equations and algebra easier to solve.

For students in class 8, it builds confidence, strengthens problem-solving skills, and lays the groundwork for advanced mathematics.

Beyond exams, factorisation is a life skill—seen in everyday tasks like sharing equally, managing time, and even in fields such as engineering and digital security.

What is Factorisation?

Factorisation (also called factoring) in mathematics means breaking down a number, algebraic expression, or polynomial into simpler parts called factors. When these factors are multiplied together, they give back the original number or expression.

• For numbers, factors are whole numbers that divide the original value exactly.
  Example: 12=3×4, 12 = 3 \times 4; So, 12=3×4, since both 3 and 4 divide evenly into 12.
• For algebraic expressions, factors are simpler terms or polynomials.
  Example: x²−4 = (x−2)(x+2), Applying the identity: a²−b²=(a−b)(a+b), because multiplying (x−2) and (x+2) gives back the original expression: (x−2)(x+2) = x²−4

Factorisation plays a key role in prime factorisation, algebraic expressions, quadratic equations, and polynomial simplification. 

For students, especially in Class 8 Maths, it is a powerful tool that makes equations easier to solve and builds the foundation for higher-level algebra.

What is the formula for factorization?

Some standard factorisation formulas you must know

1. Difference of squares:

a²–b²=(a–b)(a+b)

2. Perfect square trinomials:

(a+b)²=a²+2ab+b²
(a-b)²=a²-2ab+b²

3. Cubes (sum and difference):

a³–b³=(a–b)(a²+ab+b²)
a³+b³=(a+b)(a²–ab+b²)

4. Square of a trinomial:

(a+b+c)²=a²+b²+c²+2ab+2bc+2ca
(a–b–c)²=a²+b²+c²–2ab+2bc–2ca

5. Quadratic factorisation formula:

x²+(a+b)x+ab=(x+a)(x+b)

Remembering these factorisation formulas helps students solve algebra problems faster, especially during exams. They are also useful in higher-level maths, physics, engineering, and even real-life problem-solving, where equations need to be simplified.

For Class 8 students, mastering these formulas makes algebra less intimidating and builds confidence in solving quadratic equations and polynomial expressions.

Types of Factorisation with Examples

Factorisation in maths can be broadly divided into two types:

1. Factorisation of Numbers
2. Factorisation of Algebraic Expressions

1. Factors of Natural Numbers

When we take a natural number and express it as a product of smaller numbers, we are factorising it.

Example with 20: 20=2×10=4×5=1×20; that means 20 = 2 \times 10 = 4 \times 5 = 1 \times 20

So, the factors of 20 are 1, 2, 4, 5, 10, and 20. Out of these, 2 and 5 are prime factors. The prime factorisation of 20 is:  20=2×2×5; 20 = 2 \times 2 \times 5

Examples of prime numbers: 2, 3, 5, 7, 11, 17, 19, 23, 29.

Two common methods to find prime factors are:

• Factor Tree Method
• Division Method

Example: Prime factorisation of 100

• Using a factor tree: 100=10×10=2×5×2×5; that means 100 = 10 \times 10 = 2 \times 5 \times 2 \times 5
• Using division: divide 100 repeatedly by 2 and 5.

So, the prime factorisation of 100 is: 100=2×2×5×5

2. Factorisation of Algebraic Expressions

Factorisation of an algebraic expression means writing it as a product of simpler factors — which may be numbers, variables, or smaller expressions.

Examples:

• Expression: 2ab+3c
  • 2ab=2×a×b = 2 \times a \times b
  • 3c=3×c; 3c = 3 \times c
    Here, 2, a, and b are factors of 2ab, while 3 and c are factors of 3c.
• Expression: 2x(x+3)
  • Can be written as 2×x×(x+3); 2 \times x \times (x+3).
• Expression: 24=4×6; 24 = 4 \times 6 → factors are 4 and 6.
• Expression: 9=3×3; 9 = 3 \times 3 → factor is 3.

Methods of Factorisation in Maths

In Mathematics for Class 8 and higher, there are four main methods to factorise algebraic expressions. Each method has its own use, and with practice, you’ll know which one to apply in different situations.

These four methods of factorisation — common factors, regrouping, identities, and splitting the middle term — are the backbone of solving algebra problems. With regular practice, students can quickly identify which method makes the problem easier and faster to solve.

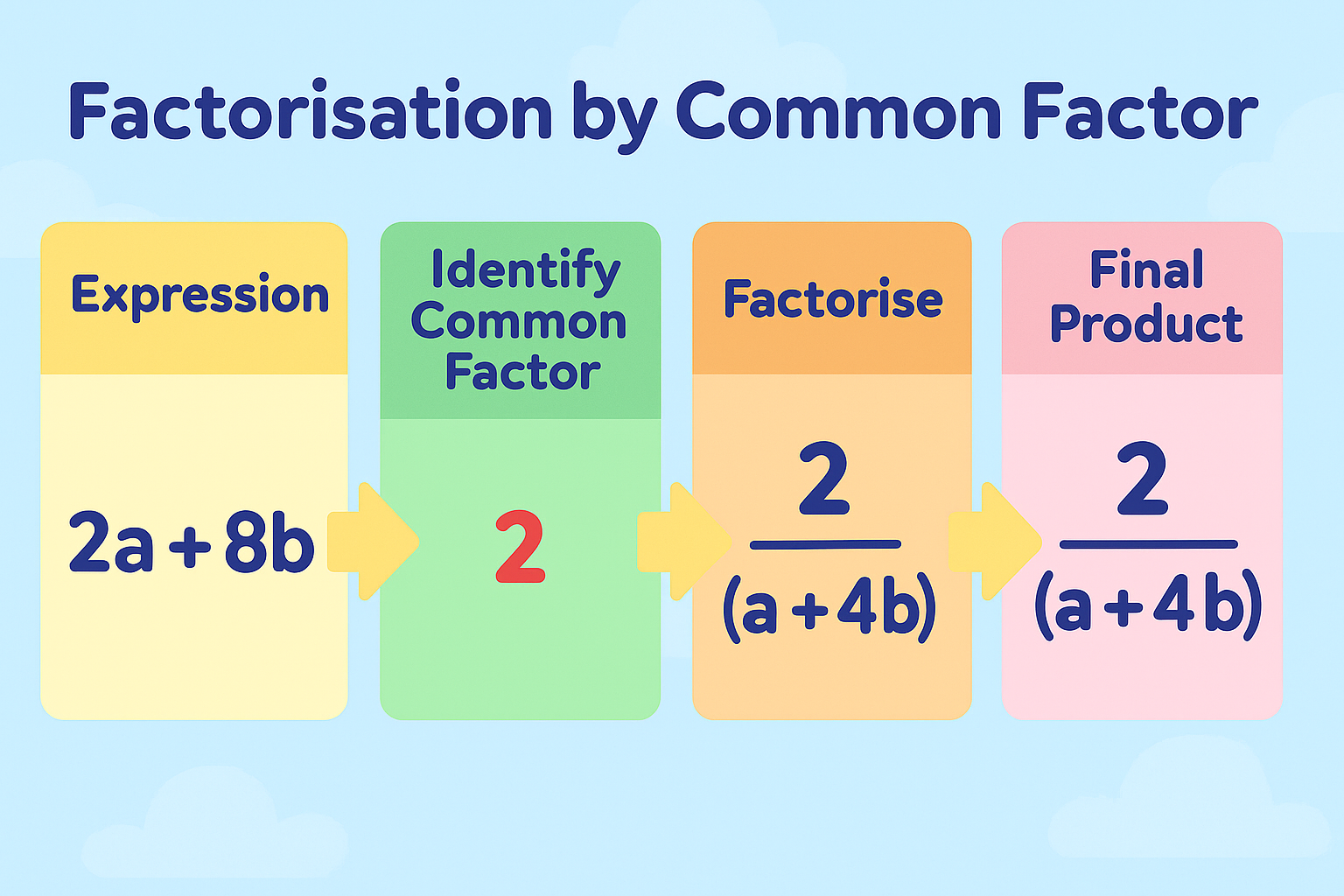
Factorisation by Common Factors

One of the simplest methods in algebraic factorisation is the Common Factors Method. In this technique, we extract the highest common factor (HCF) from all the terms of an algebraic expression and then write the expression as a product of factors.

 How It Works

1. Identify the common factor in all the terms (number, variable, or both).
2. Factor it out of the expression.
3. Write the expression as a product of the common factor and the remaining terms.

Example 1:

Expression: 3z+93z + 93z+9

Break each term:

3z+9=(3×z)+(3×3); 3z + 9 = (3 \times z) + (3 \times 3)3z+9=(3×z)+(3×3)

By applying the distributive law:

3z+9=3(z+3); 

So, the factors of 3z+93z + 93z+9 are 3 and (z + 3).

Example 2:

Expression: 2a+8b2a + 8b2a+8b

Take the common factor:

2a+8b=2(a+4b);

Here, 2 and (a + 4b) are the factors of the expression. These cannot be reduced further, so they are called irreducible factors.

Consider the expression

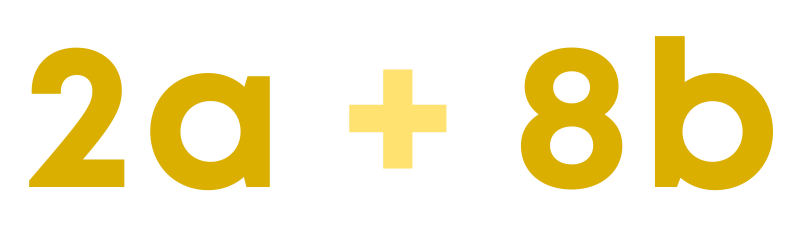
When we factorise the terms of the expression, we get

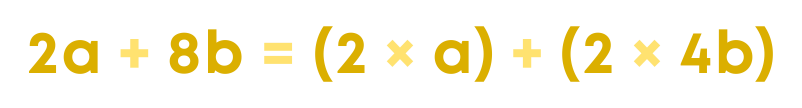
Observing the statement, by the distributive property, we have

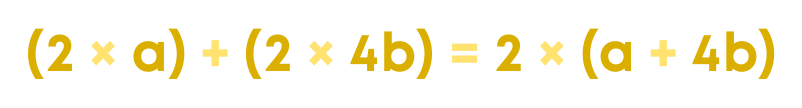
This means that 2 and (a + 4b) are the factors of the expression 2a + 8b. Can we reduce these factors further? No, we cannot. These are irreducible factors.

Factorisation by Regrouping Terms

Sometimes, an algebraic expression does not have a single common factor across all its terms. In such cases, we use the Regrouping Method of Factorisation.

By rearranging the terms, we place those with common factors side by side. This allows us to extract common factors from smaller groups and then factorise the entire expression.

 Steps to Factorise by Regrouping

1. Check for a common factor across all terms. If none exists, regroup.
2. Rearrange terms so that at least two terms in each group share a factor.
3. Take out common factors from each group.
4. Write the expression as a product of the common binomial factors.
5. Factorise completely.

Example 1:

Expression:

15ab−20b+3a−4 

Step 1: Group terms → (15ab−20b)+(3a−4); (15ab – 20b) + (3a – 4)
Step 2: Factorise each group → 5b(3a−4)+1(3a−4)
Step 3: Take out common factor → (5b+1)(3a−4)

Final Answer: (5b+1)(3a−4)

Example 2:

Expression:

21x+7y−13y²−39xy

One way to regroup:
(21x−39xy)+(7y−13y²) = 3x(7−13y)+y(7−13y)  = (3x+y)(7−13y)

Another way to regroup:
(21x+7y)−(39xy+13y²)= 7(3x+y)−13y(3x+y) = (7−13y)(x+y)

Both methods give the same factors, though the regrouping order differs.

Factorisation Using Identities

In algebra, many expressions can be simplified and factorised quickly using standard identities. These identities act like shortcuts, helping us avoid long calculations. Some of the most commonly used factorisation identities are:

a²–b²=(a–b)(a+b), (a+b)²=a²+2ab+b²
(a-b)²=a²-2ab+b²
a³–b³=(a–b)(a²+ab+b²)
a³+b³=(a+b)(a²–ab+b²)
(a+b+c)²=a²+b²+c²+2ab+2bc+2ca
(a–b–c)²=a²+b²+c²–2ab+2bc–2ca
x²+(a+b)x+ab=(x+a)(x+b)

Whenever an expression matches the form of one of these identities, we can directly write its factors.

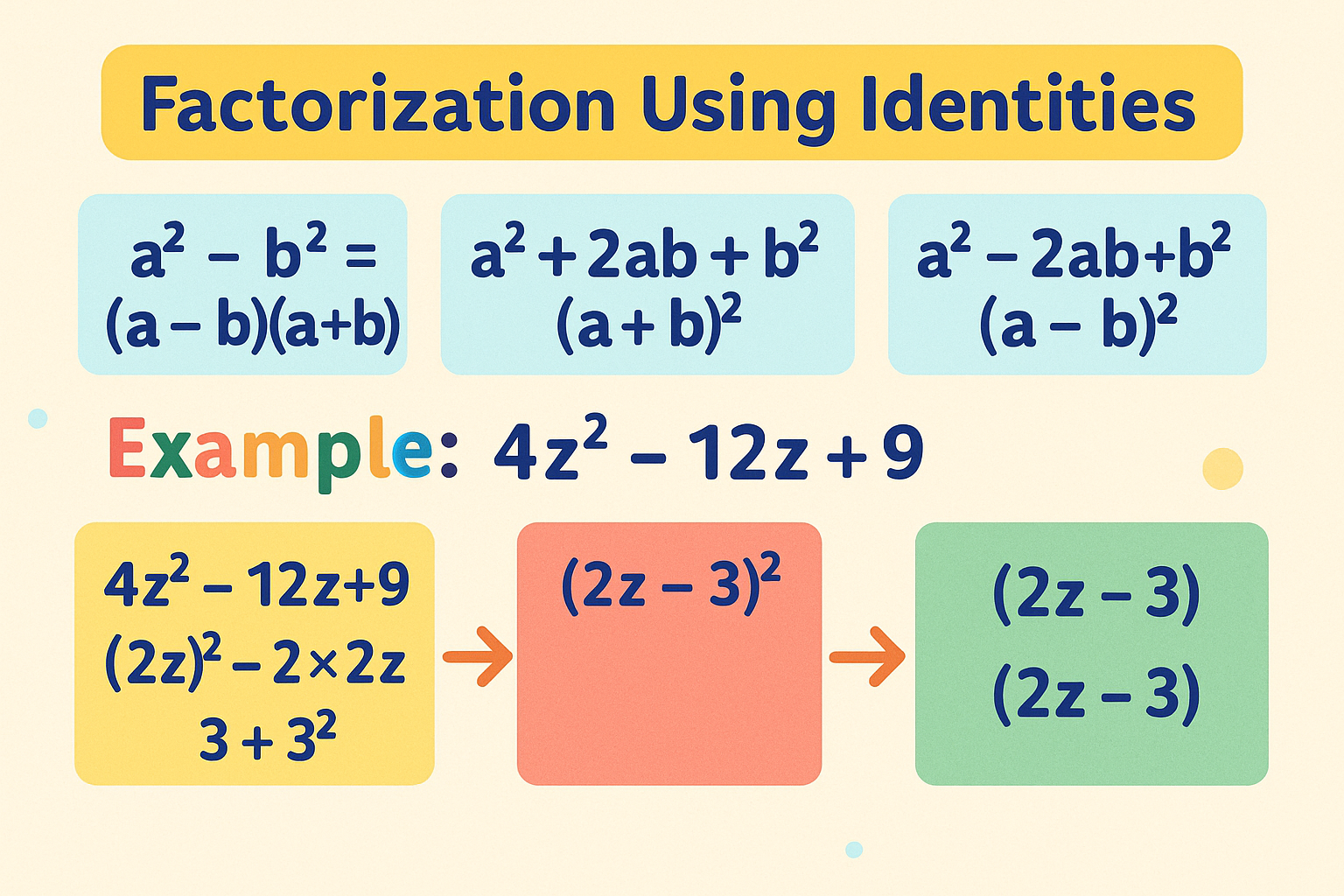
Example:

Factorise 4z²−12z+9 

Step 1: Observe the terms.

• 4z²=(2z)²
  
• 12z=2×2z×312z = 2 \times 2z \times 312z=2×2z×3
  
• 9=3²
  

Step 2: Recognise the identity. This matches the form:

a²−2ab+b²=(a−b)²

Step 3: Apply the identity.

4z²−12z+9 = (2z−3)²  

 Final Answer: The factors are (2z−3)(2z−3):

Division of Algebraic Expressions

The division of algebraic expressions is one of the most important operations in algebra. Just as multiplication and division are inverse operations for numbers, the same applies to algebraic expressions. 

Division helps us simplify complex expressions, solve equations, and even apply algebra in real-life problems like finding dimensions of shapes or missing values in formulas.

Key Idea

• Multiplication: Two factors multiply to form a product.
• Division: A product can be divided by one factor to get the other factor.

So, division is essentially the reverse of multiplication.

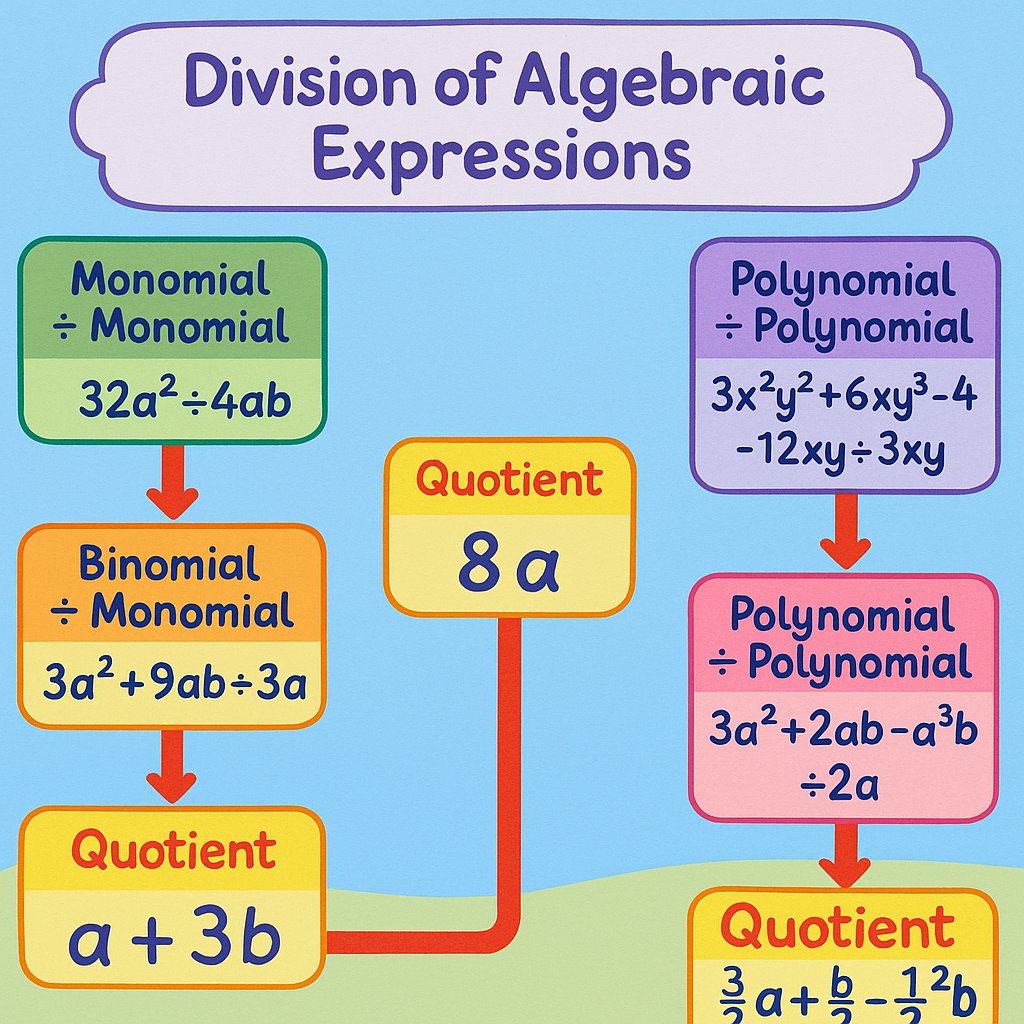
Dividing a Monomial by a Monomial

Steps:

1. Write the expression as a fraction (numerator ÷ denominator).
2. Factorise numerator and denominator.
3. Cancel out common factors.
4. The remaining factor is the quotient.

Example:

32a²b ÷ 4ab = (32 ÷ 4) × (a² ÷ a) × (b ÷ b) = 8a

Quotient = 8a

Dividing a Binomial by a Monomial

Steps:

1. Factorise each term of the binomial.
2. Cancel common factors with the divisor.
3. Simplify to get the quotient.

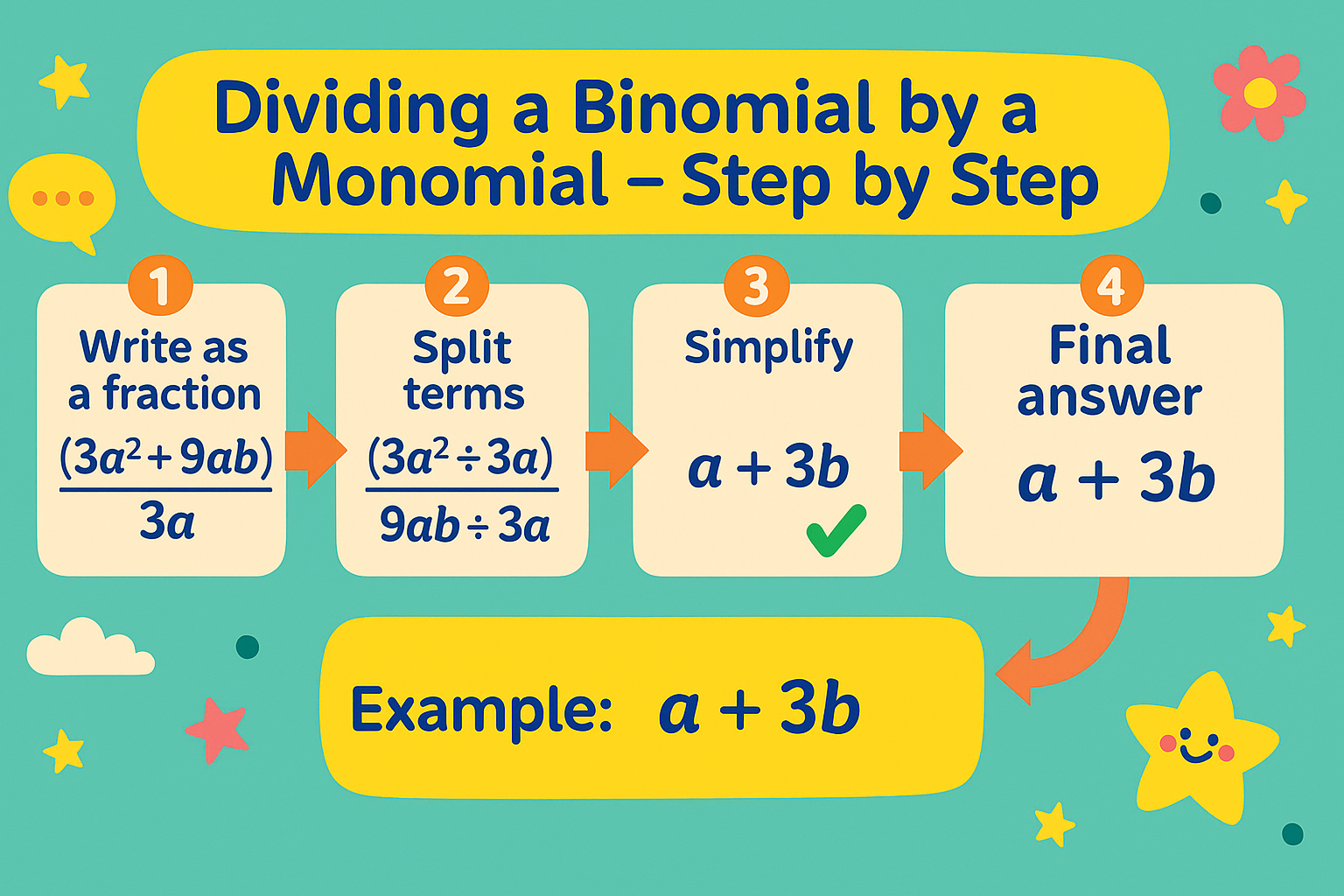
Example:

(3a² + 9ab) ÷ 3a = (3a² ÷ 3a) + (9ab ÷ 3a) = a + 3b

 Quotient = a+3b

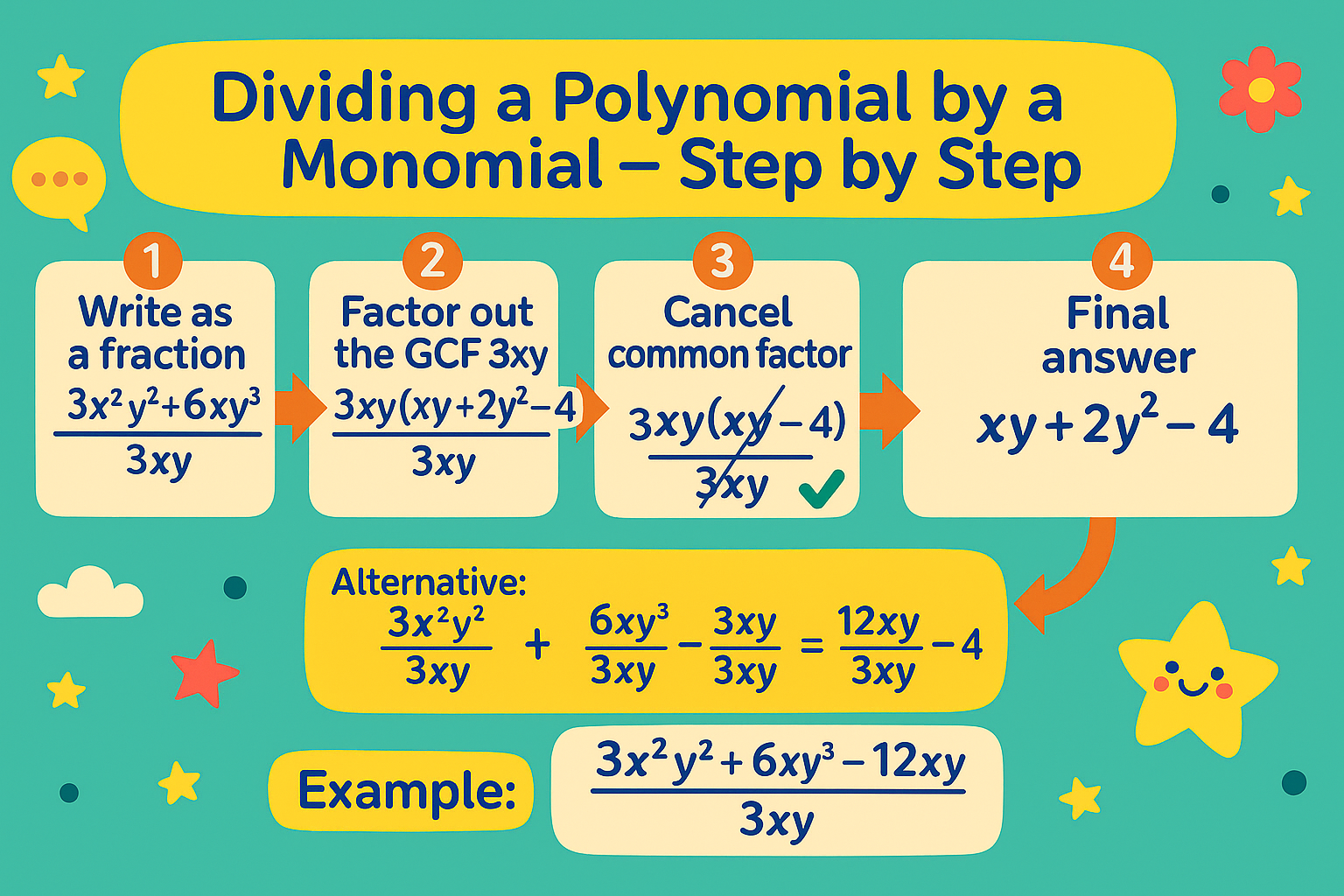
Dividing a Polynomial by a Monomial

Example:

(3x²y² + 6xy³ – 12xy) ÷ 3xy

Step 1: Factorise = 3xy(xy + 2y² – 4) ÷ 3xy
Step 2: Cancel common factor = xy + 2y² – 4
Quotient = xy+2y²−4

Dividing a Polynomial by Another Polynomial

Steps:

1. Factorise both dividend and divisor.
2. Cancel common terms.
3. The remaining factor = quotient.

Example:

(3a² + 2ab – a³b) ÷ 2a

= (3a² ÷ 2a) + (2ab ÷ 2a) – (a³b ÷ 2a)

= ³/₂ a + b – ½ a²b

 Quotient = ³/₂ a + b – ½ a²b

Applications of Division of Algebraic Expressions

• Geometry:
  • Finding the missing length/breadth of a rectangle if area and one side are given.
  • Finding the base/height of a triangle using one area and the other side.
• Factorisation: Identifying missing factors in a product.
• Algebraic Problem Solving: Simplifying polynomials to solve equations.

Evaluating Algebraic Expressions

Evaluating expressions means finding their value when certain conditions or values are given. This is where algebraic identities become very useful, as they help simplify expressions without expanding everything.
Common Identities Used

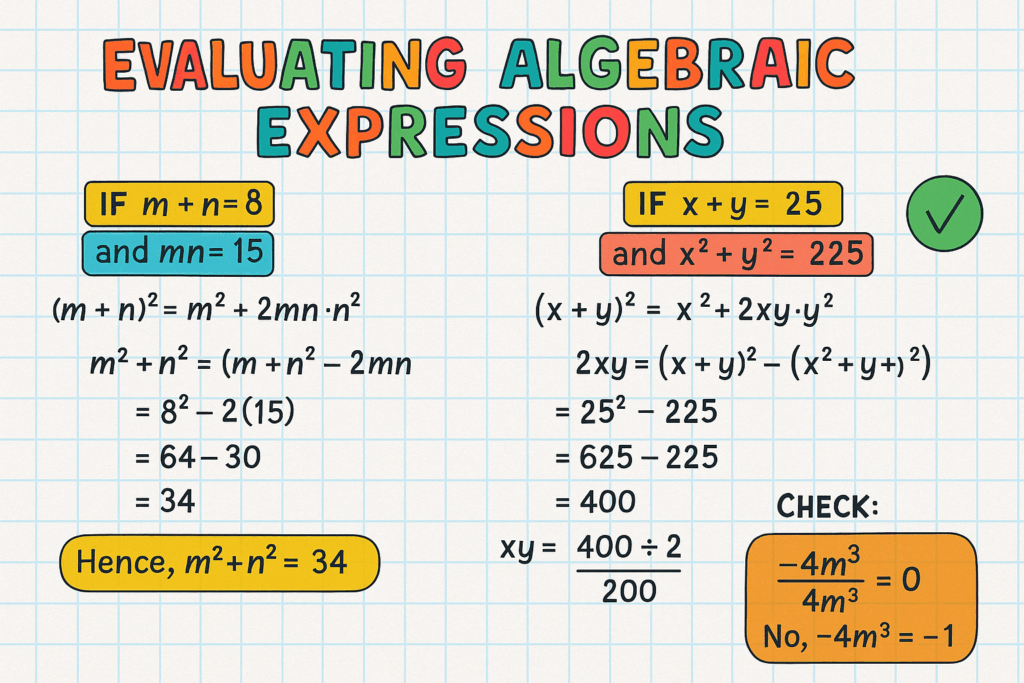
Example 1: 

Find m² + n² when m + n = 8 and mn = 15

Answer: m² + n² = (m + n)² – 2mn = 8² – 2(15) = 64 – 30 = 34

Example 2: 

If x + y = 25 and x² + y² = 225, find xy

2xy = (x + y)² – (x² + y²) = 25² – 225 = 625 – 225 = 400

Answer: xy = 200

Common Errors in Evaluating Expressions

1. Forgetting to multiply every term.
   Example: 3(2a−9) should be 6a−27, not 6a−9
2. Ignoring negative signs.
   Example: 3p−8p+11p = 6p, not 22p
3. Incorrect simplification.
   −4m³=−1\frac{-4m³} = -1, not 0.

Key Takeaways

• Always apply the correct identity before evaluating.
• Double-check signs (+/-) while adding or subtracting.
• Multiply distributively across all terms in brackets.

Why Factorisation Matters Beyond the Classroom?

Factorisation isn’t just a math exercise — it’s a tool that shapes everyday problem-solving, science, and technology. From splitting brownies to securing online transactions, it quietly powers both simple and complex systems around us.

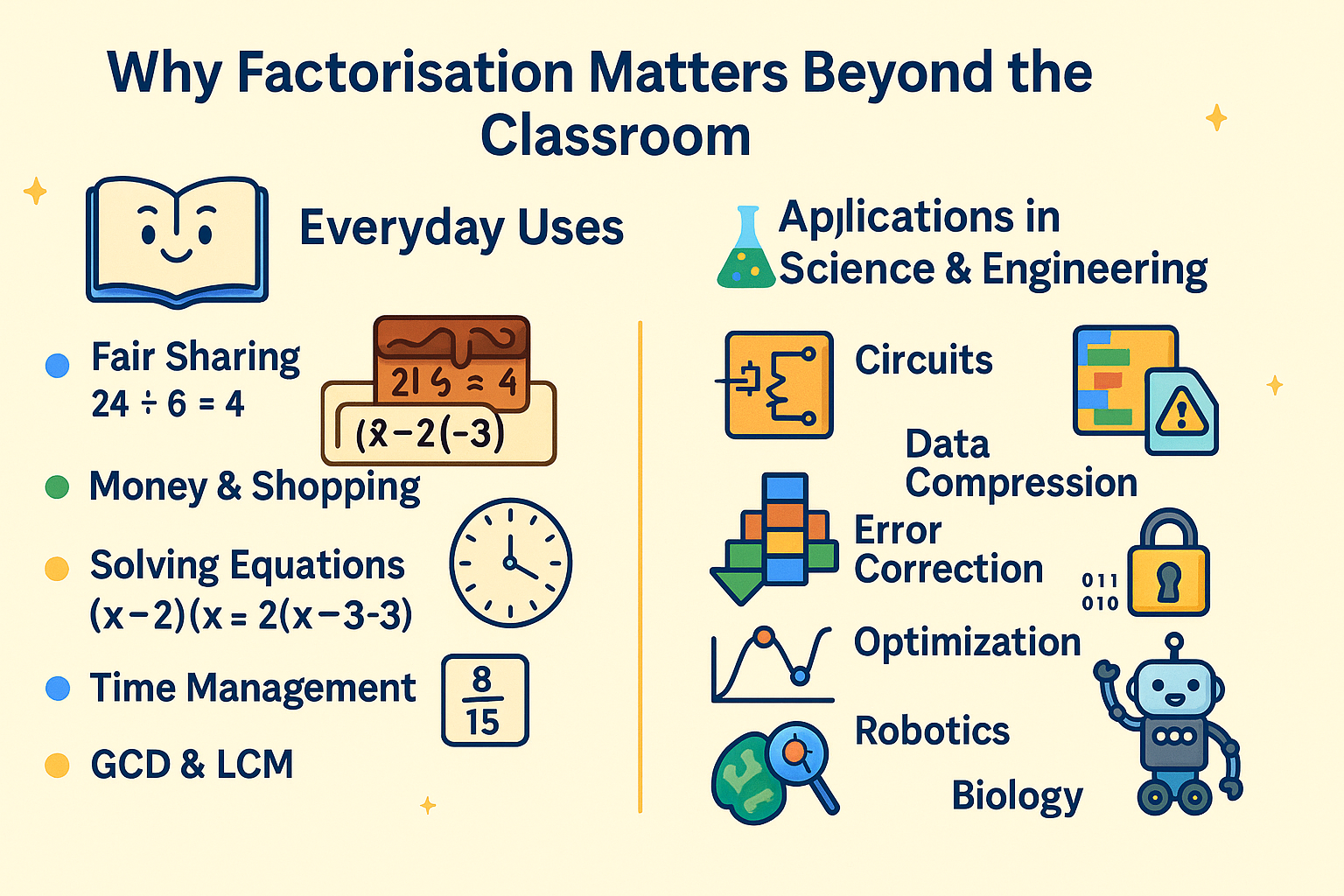
Everyday Uses:

• Fair Sharing: Dividing items equally, like splitting 24 brownies among 6 people (each gets 4).
  
• Money & Shopping: Breaking bills into smaller notes, comparing unit prices, or budgeting.
  
• Solving Equations: Factorising x2−5x+6x^2-5x+6×2−5x+6 into (x−2)(x−3)(x-2)(x-3)(x−2)(x−3) makes the roots instantly clear.
  
• Time Management: The 60 minutes in an hour split neatly into factors like 12 fives or 4 fifteens.
  
• GCD & LCM: Prime factors help simplify fractions, align timetables, or synchronise repeating cycles.
  

 Applications in Science & Engineering:

• Circuits: Engineers use factorisation to simplify polynomial models of electrical systems.
  
• Data Compression: Identifying repeating patterns through factorisation helps shrink file sizes.
  
• Error Correction: Digital codes factorise polynomials to detect and fix transmission errors.
  
• Cryptography: Encryption methods like RSA rely on the difficulty of factoring very large numbers.
  
• Optimization: Used in logistics, manufacturing, and finance to allocate resources efficiently.
  
• Robotics: Polynomial factorisation supports path planning and energy-efficient movements.
  
• Biology: Genetic modelling often involves factoring polynomial equations.

In short: factorisation is the hidden engine of order and efficiency — helping us divide, solve, optimise, and secure the systems we rely on every day.

How to Prevent Common Errors in Factorization?

Factorisation is one of those math skills where a small slip can throw off the entire solution. Most errors happen because we rush or overlook simple checks. Here are the mistakes students make most often — and how to avoid them.

• Skipping the Common Factor

Many students jump straight into tricky steps without first pulling out the Greatest Common Factor (GCF). This makes the problem harder and often leaves the factorisation incomplete.
Always start by asking: What’s common in all terms?

• Forgetting or Misusing Identities

Formulas like

• a²−b²=(a−b)(a+b)
  
• a²+2ab+b²=(a+b)²  are lifesavers — but they’re often forgotten or applied incorrectly.
    Keep these identities handy and practice spotting them in expressions.
  
•  Wrong Signs in the Middle Term

When splitting the middle term in a quadratic, one wrong sign can ruin the whole answer.
Double-check: do your chosen numbers both multiply to and add to?

•  Mixing Up Factorisation with Simplification

Factorising means breaking an expression into factors — not just reducing or simplifying it. Stopping too early or missing a further step leaves the work incomplete.

•  Writing “1” as a Factor

Yes, 1 is technically a factor of everything — but writing it out only clutters the solution and causes confusion. Leave it out.

•  Errors in Algebraic Expressions

• Not spotting all common factors.
• Choosing the wrong pair of numbers when splitting the middle term.
• Making calculation slips when substituting values after factorisation.
  

Quick Fix:

1. Always check for a common factor first.
2. Spot patterns and identities.
3. Be careful with signs.
4. Don’t stop until fully factored.
5. Re-expand your factors to check if they match the original expression.

 Factorisation is like solving a puzzle — if you use the right strategy and avoid these traps, the pieces will fall into place.

Practice Exercises and Answers on Factorization with Gonit App

Gonit is a math app designed to help students practice and improve their problem-solving skills, including factorisation. The app offers step-by-step answers and practice problems, making it easier to learn and master topics like factorisation through interactive challenges and detailed solutions.

With Gonit, users can:

• Access a wide range of factorisation practice problems tailored to different grade levels.
• Get instant step-by-step solutions to understand how each factorisation problem is solved.
• Practice progressively from simple to advanced factorisation challenges.
• Prepare effectively for math Olympiads and competitions with focused exercises.

If looking to easily practice factorisation problems and solutions with guided help, Gonit is a useful app to consider for continual learning and exam preparation.

Final Thoughts and Key Learnings on Factorisation in Class 8 Maths

Mastering factorisation in Class 8 mathematics is more than just learning formulas—it’s about developing problem-solving skills that make algebra easier and more enjoyable.

By understanding different methods of factorisation—whether through prime factorisation, algebraic identities, or regrouping terms—students build a strong foundation for higher-level topics in algebra, geometry, and even real-life applications like simplifying calculations or logical reasoning.